The Reproducing Kernel Element Method (RKEM) is the first method to
provide minimal higher order globally compatible basis functions in
any spatial dimension.
RKEM Shape Functions
The following plots display the shape functions for 3 node
triangles.
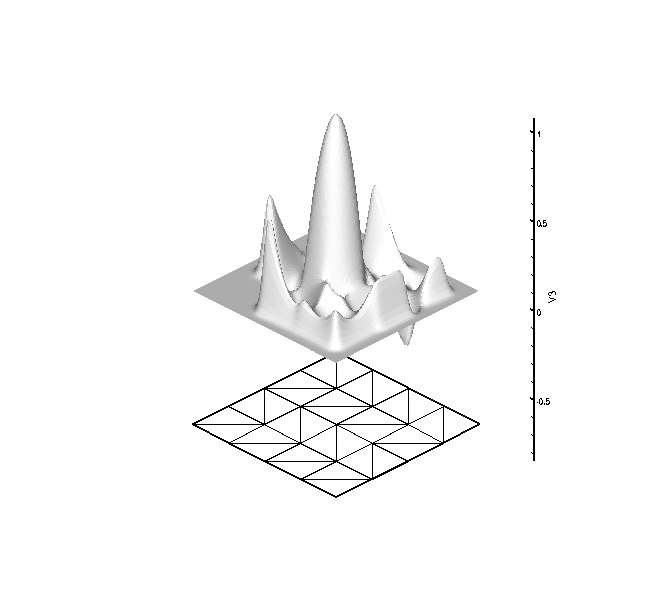
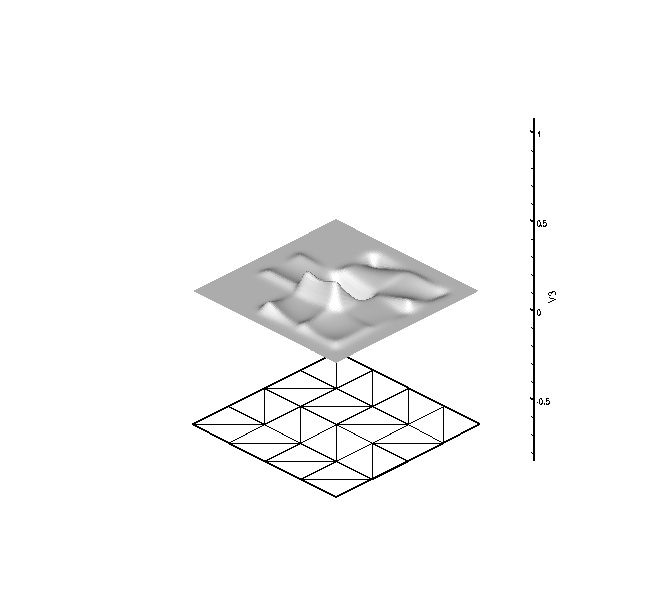
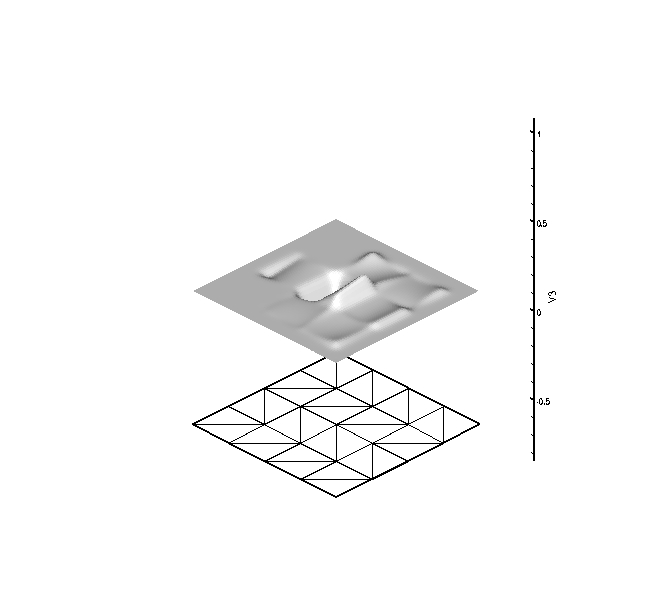
The first set of plots have 3 DOF per node, are globally C^4
continuous, and globally reproduce quadratic polynomials. The three
figures correspond to the shape function associated with each DOF
shown above the mesh upon which they are computed.
 |
 |
 |
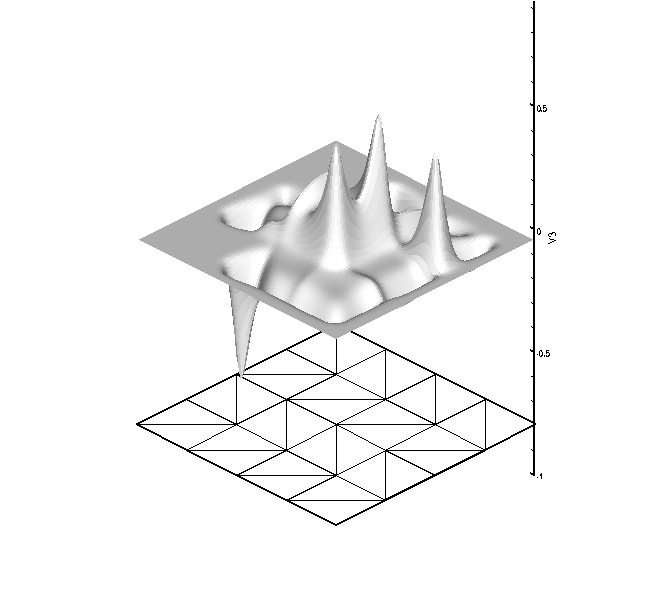
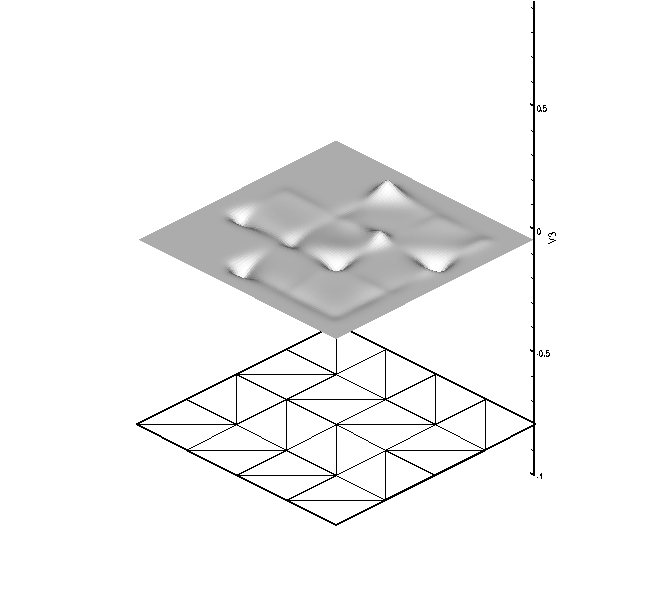
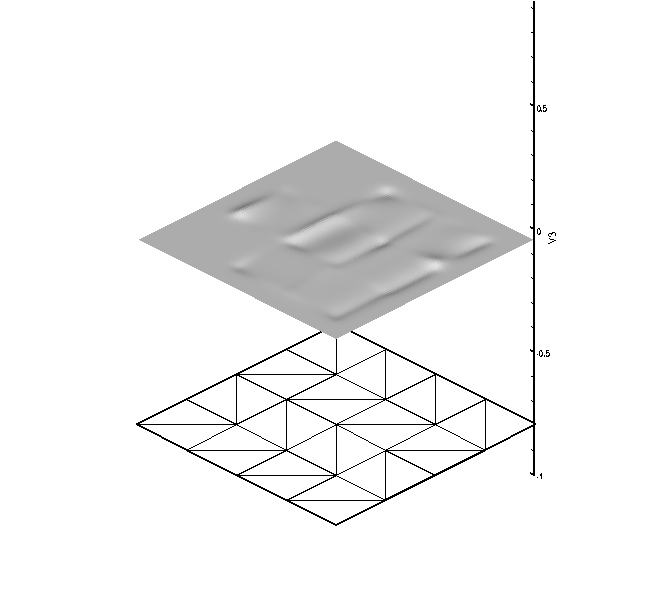
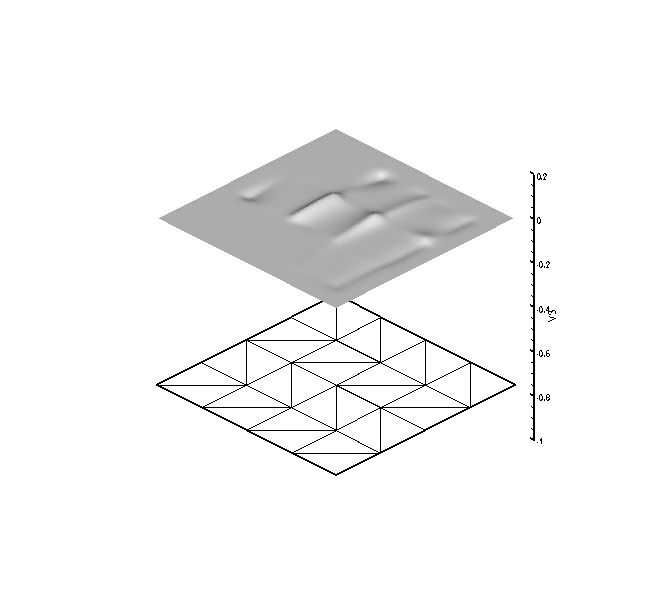
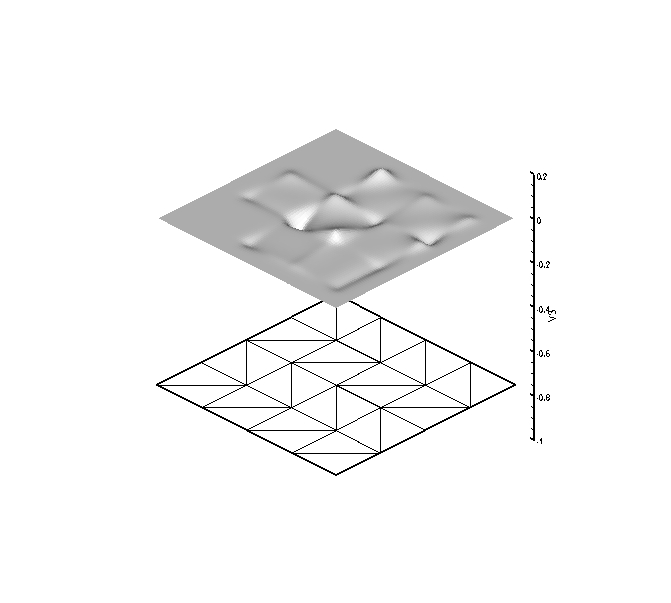
The next set of plots have 6 DOF per node, are globally C^4
continuous, and globally reproduce quartic polynomials. The six
figures correspond to the shape function associated with each DOF
shown above the mesh upon which they are computed.
 |
 |
 |
 |
 |
 |
RKEM Galerkin Solutions
Here are a few examples showing the performance of RKEM shape
functions in Galerkin solutions of the biharmonic. In these examples,
we are solving the Kirchhoff plate equation (biharmonic) for fixed and
simply-supported boundary conditions loaded with a uniform
pressure. Note that the weakform of the biharmonic contains two
derivatives, and hence requires C^1 continuity. Standard C^0 finite
elements cannot solve this problem.
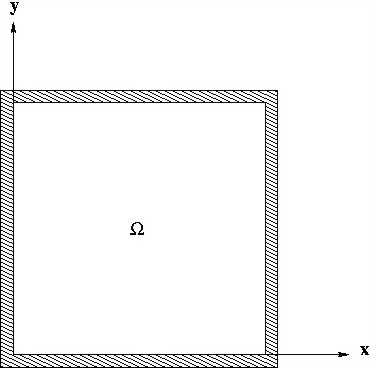
Clamed Square Plate
 |
 |
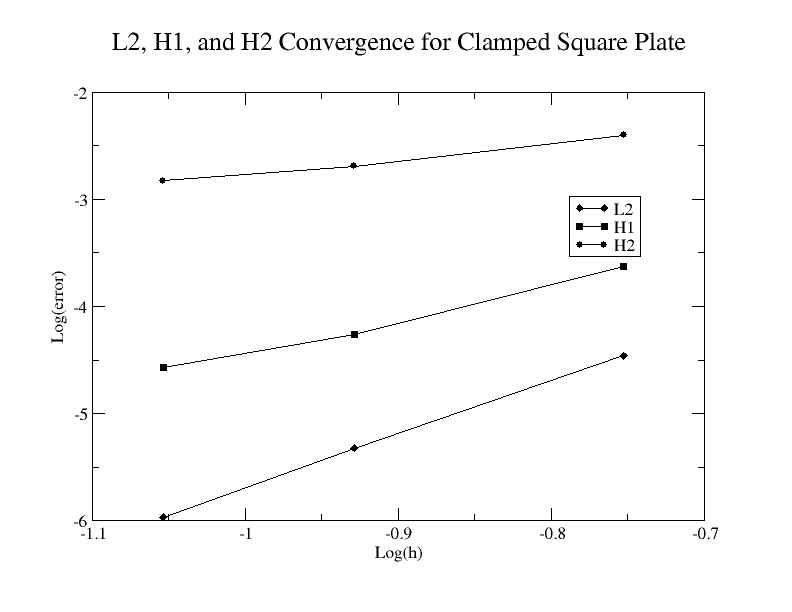 |
These show the problem domain, displaced shape, and convergence. The L2 convergence for this problem is 5.007.
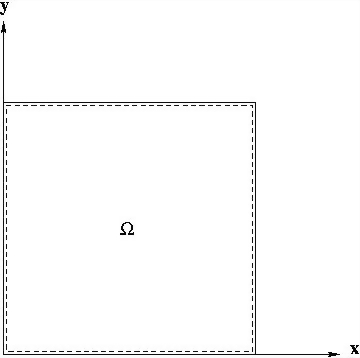
Simply Supported Square Plate
 |
 |
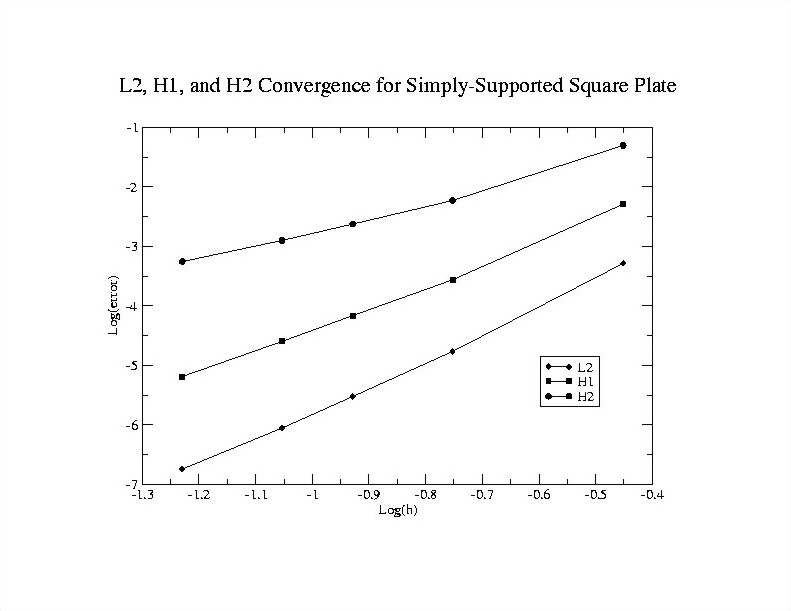 |
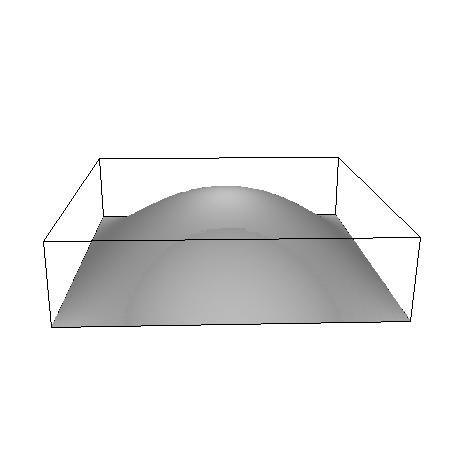
These show the problem domain, displaced shape, and convergence. The L2 convergence for this problem is 4.4506.















