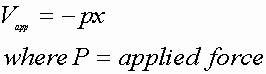For certain classification of forces, called Conservative forces, the work-energy relationship becomes an even easier expression. Conservative forces are defined as forces with only two stipulations:

1. i.e. the forces are at most a function of position

2. F can be expressed as a gradient of a scalar function

Then

i.e. The integral representing the work done on the particle, for conservative forces, is only dependent on the value of the scalar function at the final position, and then initial position, and NOT on the shape of the path. We now define potential energy, V, as the negative of the scalar function.

Thus, for cases involving conservative forces, the work energy relationship becomes.

T₁ = Total Kinetic Energy at Position 1

V₁= Total Potential Energy at Position 1

T₂ = Total Kinetic Energy at Position 2

V₂= Total Potential Energy at Position 2

Facts:

1. C.M.E. is only valid for conservative forces,

2. Friction is the major non-conservative force

3. Anytime C.M.E. is used a datum must be established.

a. The location of the datum is arbitrary

4. F is conservative if and only if curl 

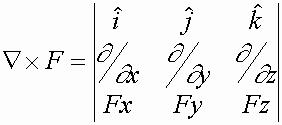
5. Potential Energy is due to gravity

b. Vsp is always positive

7. Potential Energy of an applied force